Chapter 10: Mirror Reflection
10.1 The physics of mirror reflection
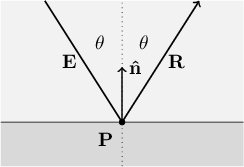
Like refraction, mirror reflection is a phenomenon that occurs at the boundary between two substances. In both cases, a portion of a light ray's energy is sent in a new direction when that ray hits a point on the boundary. Unlike refraction, mirror reflection causes light to bend back into the substance from which it came, instead of bending along a path into the new substance. Mirror reflection is also mathematically much simpler than refraction. The refractive indices of the two substances affect the amount of reflected light, but they have nothing to do with the reflected light's direction: light always reflects at the same angle as it arrived, as mesured from a line perpendicular to the surface. Just as we saw with refraction, the reflected ray lies in the same plane as both the incident ray and the perpendicular line, only on the opposite side of the perpendicular line as the incident ray. See Figure 10.1.
|
Figure 10.1: The incident ray $\mathbf{E}$ strikes the boundary between two substances at point $\mathbf{P}$. The ray reflects in the direction $\mathbf{R}$. The rays $\mathbf{E}$ and $\mathbf{R}$ both extend the same angle $\theta$ from the surface's perpendicular. |
|
10.2 Two kinds of reflection, same vectors
In Chapter 7, we learned that this ray tracer source code models mirror reflection as the sum of two separate kinds of reflection: glossy reflection and refractive reflection. To recap, glossy reflection belongs to an imaginary coating on an object's surface. Refractive reflection, however, is determined by the refractive indices of substances on opposite sides of their common boundary. Glossy reflection may vary across an object's surface, but is equal in intensity regardless of the angle of the light's incidence; refractive reflection is more intense for light rays that arrive at a larger angle from the perpendicular. Glossy reflection can impart a color bias onto reflected light, but refractive reflection bounces red, green, and blue light equally.
In spite of all of these differences, they share an important geometrical trait. In both kinds of mirror reflection, the same incident ray $\mathbf{E}$ results in a reflected ray traveling in exactly the same outgoing direction $\mathbf{R}$, as depicted in Figure 10.1. For this reason, the ray tracer code calculates the intensities and colors of glossy reflection and refractive reflection separately, but adds them together and calculates their common direction $\mathbf{R}$ using a single member function CalculateReflection.
10.3 Deriving the vector formula
|
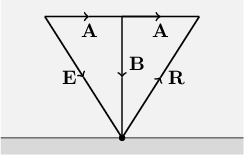
Figure 10.2: Vectors used in the derivation of the reflection formula. |
|
We now consider the problem of calculating the mirror reflection vector $\mathbf{R}$, given the incident light ray vector $\mathbf{E}$ and the surface normal vector $\mathbf{\hat{n}}$. The first step is to break $\mathbf{E}$ into the sum of two vectors $\mathbf{A}$ and $\mathbf{B}$, such that $\mathbf{A}$ is parallel to the reflective surface and $\mathbf{B}$ is perpendicular to it, as depicted in Figure 10.2. Reflected light bounces away from the surface at the same angle as the incident light, so the angle between $\mathbf{E}$ and $\mathbf{B}$ is the same as the angle between $\mathbf{R}$ and $\mathbf{B}$. Two symmetric right triangles appear: $\mathbf{A}\mathbf{B}\mathbf{E}$ and $\mathbf{A}\mathbf{B}\mathbf{R}$.
We can see from Figure 10.2 that the following two vector equations must be true. (Initially, the second equation might be easier to understand rewritten as $\mathbf{B} + \mathbf{R} = \mathbf{A}$, but the form below is more useful to the upcoming discussion.)
\begin{align*}
\mathbf{E} &= \mathbf{A} + \mathbf{B} \\
\mathbf{R} &= \mathbf{A} - \mathbf{B}
\end{align*}
We can find the perpendicular vector $\mathbf{B}$ by noting that since it is the component of $\mathbf{E}$ perpendicular to the surface, its magnitude must be equal to the dot product of $\mathbf{E}$ and the surface normal vector $\mathbf{\hat{n}}$. Likewise, $\mathbf{B}$ must point in either the same direction as $\mathbf{\hat{n}}$ or in the opposite direction $-\mathbf{\hat{n}}$. Regardless of the orientation of the $\mathbf{\hat{n}}$ (i.e., whether this reflection is occurring on the outside surface or inside surface of an instance of SolidObject), the following equation works.
\[
\mathbf{B} = (\mathbf{E}\cdot\mathbf{\hat{n}}) \mathbf{\hat{n}}
\]
To convince you that this equation works in both cases, consider each case separately. If $\mathbf{\hat{n}}$ points in the opposite direction as $\mathbf{B}$ (or upward as seen in Figure 10.2), then $\mathbf{E}\cdot\mathbf{\hat{n}}$ is a negative number, and multiplying any vector by a negative number results in another vector pointing in the opposite direction. Thus $(\mathbf{E}\cdot\mathbf{\hat{n}})\mathbf{\hat{n}}$ points in the same direction as $\mathbf{B}$. Alternatively, if $\mathbf{\hat{n}}$ points in the same direction as $\mathbf{B}$ (downward as seen in the figure), the dot product is a positive number, and therefore $(\mathbf{E}\cdot\mathbf{\hat{n}})\mathbf{\hat{n}}$ still points in the same direction as $\mathbf{B}$.
We now substitute the value of $\mathbf{B}$ into the equations for $\mathbf{E}$ and $\mathbf{R}$.
\begin{align*}
\mathbf{E} &= \mathbf{A} + (\mathbf{E}\cdot\mathbf{\hat{n}})\mathbf{\hat{n}} \\
\mathbf{R} &= \mathbf{A} - (\mathbf{E}\cdot\mathbf{\hat{n}})\mathbf{\hat{n}}
\end{align*}
Subtracting the first equation from the second results in $\mathbf{A}$ canceling out, and adding $\mathbf{E}$ to both sides of this new equation results in the following formula for the reflected ray $\mathbf{R}$:
\[
\mathbf{R} = \mathbf{E} - 2 (\mathbf{E}\cdot\mathbf{\hat{n}})\mathbf{\hat{n}}
\]
This is exactly what we wanted. We now know how to calculate $\mathbf{R}$ using only $\mathbf{E}$ and $\mathbf{\hat{n}}$.
10.4 Recursive call to CalculateLighting
Once CalculateReflection uses the preceding formula to calculate the direction of the reflected ray, it must figure out where that ray goes in order to determine what effect the ray has on the image. The intersection point where the ray reflected becomes a new vantage point, and the reflected ray direction $\mathbf{R}$ becomes the new direction to look.
CalculateReflection calls TraceRay to search in the direction $\mathbf{R}$ from the new vantage point $\mathbf{P}$. If TraceRay finds an intersection in that direction, it calls CalculateLighting to complete the evaluation of the reflected ray. Because CalculateLighting and CalculateReflection call each other through the intermediate function TraceRay, their mutual recursion must be protected from excessive call depth. TraceRay thus adds 1 to whatever recursion depth is passed to it and sends that increased value to CalculateLighting. The latter stops the recursion if the maximum allowed depth has been reached.
As in any other case, if TraceRay finds no intersection in the specified direction, it knows that the ray continues infinitely into space and therefore returns the background color diminished by the ray intensity that was passed into it. Recall that the rayIntensity parameter tracks how weak the red, green, and blue color components of a ray of light have become as the ray bounces around the scene.
10.5 CalculateReflection source code
Color Scene::CalculateReflection(
const Intersection& intersection,
const Vector& incidentDir,
double refractiveIndex,
Color rayIntensity,
int recursionDepth) const
{
// Find the direction of the reflected ray based on the incident ray
// direction and the surface normal vector. The reflected ray has
// the same angle with the normal vector as the incident ray, but
// on the opposite side of the cone centered at the normal vector
// that sweeps out the incident angle.
const Vector& normal = intersection.surfaceNormal;
const double perp = 2.0 * DotProduct(incidentDir, normal);
const Vector reflectDir = incidentDir - (perp * normal);
// Follow the ray in the new direction from the intersection point.
return TraceRay(
intersection.point,
reflectDir,
refractiveIndex,
rayIntensity,
recursionDepth);
}
Copyright © 2013 by
Don Cross.
All Rights Reserved.