 |
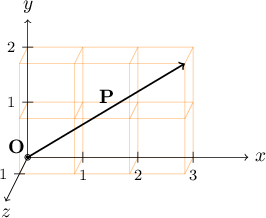
Figure 4.1: The vector $\mathbf{P} = (3,2,1)$. The origin is labeled $\mathbf{O}$. |
Before diving into the details of the ray tracing algorithm, the reader must have a good understanding of vectors and scalars. If you already feel comfortable with vectors, scalars, and mathematical operations involving them, such as a vector addition and subtraction, multiplying a vector with a scalar, and vector dot products and cross products, then you can skip this chapter and still understand the subsequent material. This chapter is not intended as an exhaustive treatment of vector concepts, but merely as a summary of the topics we need to understand ray tracing.
A scalar is a number like $3.7$ or $-14.25$. A scalar may be negative, positive, or zero. We use the word "scalar" to describe such numbers primarily so we can distinguish them from vectors.
A vector is a triplet of numbers that can represent the location of a point in three-dimensional space or a direction in space from a given starting point. A vector is written as $(x, y, z)$ where $x$, $y$, and $z$ are real numbers called components or coordinates. The $x$, $y$, and $z$ components indicate how far, and which way, to move along three perpendicular lines to arrive at a point. The perpendicular lines are called axes (the plural; the singular form is axis).
The starting point where the $x$, $y$, and $z$ axes intersect is called the origin. At the origin, the values of $x$, $y$, and $z$ are all zero, so the origin can be written as $(0, 0, 0)$. In Figure 4.1, starting at the origin $\mathbf{O}$, the vector $\mathbf{P} = (3, 2, 1)$ takes us 3 units to the right (or "east" if you prefer), 2 units toward the top of the page ("north") and 1 unit directly out from the page toward you ("up").
| |
|
Note that we can look at the $x$, $y$, and $z$ axes from many different points of view. For example, we could let $x$ point southeast and $y$ point northeast. But not only do the $x$, $y$, and $z$ axes have to be at right angles to each other, but the directions that any two of the axes point determine the direction the third axis must point. An easy way to visualize this requirement is to imagine your head is at the origin and that you are looking in the direction of the $x$ axis, with the top of your head pointing in the direction of the $y$ axis. In this case the $z$ axis must point to your right; it is not allowed to point to your left. This convention is arbitrary, but consistently following it is necessary in the mathematics and algorithms to come; otherwise certain vector operations will give wrong answers. (See also: Wikipedia's article Right-hand rule.)
Suppose that we start at the origin, but this time take a slightly more complicated journey.
| |
|
First we follow the vector $\mathbf{A}$ to move 2 units east, 2 units north, and 1 unit up. Then, starting from that point we move along the vector $\mathbf{B}$ and travel 2 more units east, one unit south (the same as $-1$ units north) and 1 unit down ($-1$ units up). We end up at a location specified by adding the respective $x$, $y$, and $z$ components of the vectors $\mathbf{A}$ and $\mathbf{B}$, namely $(2+2, 2+(-1), 1+(-1)) = (4, 1, 0)$. (See Figure 4.2.) If we call our final position $\mathbf{C}$, we can write concisely in vector notation that
\[ \mathbf{A} + \mathbf{B} = \mathbf{C} \]
or
\[ (2, 2, 1) + (2, -1, -1) = (4, 1, 0). \]
It would not matter if we reversed the order of the vectors— if we went from the origin in the direction specified by the $\mathbf{B}$ vector first, then from there in the direction specified by the $\mathbf{A}$ vector, we would still end up at $\mathbf{C}$. So vectors added in either order, $\mathbf{A}+\mathbf{B}$ or $\mathbf{B}+\mathbf{A}$, always produce the same result, just like scalars can be added in either order to obtain the same scalar result. Said in more formal mathematical terms, vector addition and scalar addition are both commutative. In general, if
\[ \mathbf{A} = (A_x, A_y, A_z) \]
and
\[ \mathbf{B} = (B_x, B_y, B_z) \]
then
\[ \mathbf{A} + \mathbf{B} = (A_x + B_x, A_y + B_y, A_z + B_z). \]
Similarly, we can define vector subtraction by
\[ \mathbf{A} - \mathbf{B} = (A_x - B_x, A_y - B_y, A_z - B_z). \]
One helpful interpretation of vector subtraction is to imagine starting at the origin and moving along the vector $\mathbf{A}$ (as we did before for vector addition) but then moving in the opposite direction as specified by $\mathbf{B}$. For example, re-using $\mathbf{B} = (2, -1, -1)$, we would move 2 units west (instead of east), 1 unit north (instead of south), and 1 unit up (instead of down), to arrive at $(2-2, 2-(-1), 1-(-1)) = (0, 3, 2)$, labeled as $\mathbf{D}$ in Figure 4.3.
| |
|
Another important interpretation of vector subtraction is that it calculates a vector that takes us from one location to another location. Suppose we are located at the point $\mathbf{E} = (1, 3, 0)$ and we want to know how to travel to the point $\mathbf{F} = (5, 2, 0)$. Another way to pose this question is to ask, what is the vector $\mathbf{G}$ such that $\mathbf{E} + \mathbf{G} = \mathbf{F}$? In algebra with scalars, we could subtract $\mathbf{E}$ from both sides of the equation and determine that $\mathbf{G} = \mathbf{F} - \mathbf{E}$. It turns out that this approach is just as valid when applied to vectors. So in our current example, $\mathbf{G} = \mathbf{F} - \mathbf{E} = (5, 2, 0) - (1, 3, 0) = (5-1, 2-3, 0-0) = (4, -1, 0)$. Looking at Figure 4.4, it makes sense that if we start at $\mathbf{E}$, move 4 units east, 1 unit south, and 0 units up, we end up at $\mathbf{F}$.
| |
|
Suppose we want to start at the origin point $(0, 0, 0)$ and move in the direction of some vector $\mathbf{A}$, but move 3 times as far as $\mathbf{A}$ goes? Based on what we have seen so far, we could calculate $\mathbf{A}+\mathbf{A}+\mathbf{A}$. If we were dealing with a scalar quantity, we would immediately be able to simplify this as $\mathbf{A}+\mathbf{A}+\mathbf{A} = 3\mathbf{A}$. Does this work for vectors? Let's find out.
\begin{align*} & \mathbf{A} + \mathbf{A} + \mathbf{A} \\ = & (A_x, A_y, A_z) + (A_x, A_y, A_z) + (A_x, A_y, A_z) \\ = & (A_x + A_x + A_x, A_y + A_y + A_y, A_z + A_z + A_z) \\ = & (3 A_x, 3 A_y, 3 A_z) \end{align*}
If we allow ourselves to write the final vector as $(3 A_x, 3 A_y, 3 A_z) = 3\mathbf{A}$, then we have behavior for vectors that matches the familiar rules of scalar algebra. In general, we define multiplication of a scalar $u$ and a vector $\mathbf{A}$ as
\[ u\mathbf{A} = u(A_x, A_y, A_z) = (u A_x, u A_y, u A_z) \]
where $u$ is any scalar value, whether negative, positive, or zero. If $u=0$, the resulting product $u\mathbf{A}=(0,0,0)$, no matter what the values of $A_x$, $A_y$, and $A_z$ are. Another way to think of this is that moving zero times in any direction is the same as not moving at all. Multiplying $u=-1$ by a vector is the same as moving the same distance as that vector, but in the opposite direction. We can write $(-1)\mathbf{A}$ more concisely as $-\mathbf{A}$.
Sometimes we will have a vector and need to know how long it is. The length of a vector is called its magnitude. Mathematicians express the magnitude of a vector by writing it between two vertical bars. So the magnitude of a vector $\mathbf{A}$ is written like this: $\lvert\mathbf{A}\rvert$. $\lvert\mathbf{A}\rvert$ is a scalar, because it is just a simple number. If $\mathbf{A} = (A_x, A_y, A_z)$, then $\lvert\mathbf{A}\rvert$ can be calculated using the Pythagorean Theorem as
\[ \lvert\mathbf{A}\rvert = \sqrt{A_x^2 + A_y^2 + A_z^2} \]
For example, if $\mathbf{A} = (3, -1, 2)$, then
\[ \lvert\mathbf{A}\rvert = \sqrt{3^2 + (-1)^2 + 2^2} = \sqrt{14} = 3.7416... \]
Sometimes it will be handy to use a vector to specify a direction in space while requiring the vector's magnitude to be exactly equal to 1. We call any vector whose magnitude is 1 a unit vector. If we have an arbitrary vector $\mathbf{A} = (A_x, A_y, A_z)$ and want to find a unit vector $\hat{v}$ that points in the same direction, we can do this by dividing the vector $\mathbf{A}$ by its scalar length $\lvert\mathbf{A}\rvert$:
\[ \hat{v} = \frac{\mathbf{A}}{\lvert\mathbf{A}\rvert} = \left( \frac{A_x}{\lvert\mathbf{A}\rvert}, \frac{A_y}{\lvert\mathbf{A}\rvert}, \frac{A_z}{\lvert\mathbf{A}\rvert} \right) \]
where again, $\lvert\mathbf{A}\rvert = \sqrt{A_x^2 + A_y^2 + A_z^2}$. (Throughout this text, I will use a lowercase letter with a caret over it to represent unit vectors, so if you see a variable like $\hat{v}$, you can assume that $\lvert\hat{v}\rvert = 1$.) The only case where the above magnitude formula fails is when $\mathbf{A} = (0, 0, 0)$, because we would end up trying to divide by 0. It makes sense that $(0, 0, 0)$ does not "point" in any particular direction, so it is the one case where it becomes meaningless to speak of an associated unit vector.
A useful question we can ask about two different vectors $\mathbf{A}$ and $\mathbf{B}$ is, do $\mathbf{A}$ and $\mathbf{B}$ point in the same direction, opposite directions, are they perpendicular to each other, or are they somewhere between these special cases? There is a surprisingly easy way to answer this question, though explaining why it works is beyond the scope of this book.
By multiplying each of the three components of $\mathbf{A}$ with the corresponding component of $\mathbf{B}$, and adding up the three resulting products, we obtain a sum called the dot product of the vectors $\mathbf{A}$ and $\mathbf{B}$, so called because mathematicians write a dot "$\cdot$" between them:
\[ \mathbf{A}\cdot\mathbf{B} = (A_x, A_y, A_z)\cdot(B_x, B_y, B_z) = A_x B_x + A_y B_y + A_z B_z \]
Note that although $\mathbf{A}$ and $\mathbf{B}$ are both vectors, their dot product is a scalar. For this reason, some authors will refer to this operation as the scalar product of the two vectors. It turns out that if $\mathbf{A}$ and $\mathbf{B}$ are perpendicular to each other, their dot product $\mathbf{A}\cdot\mathbf{B}$ will be 0. As a simple example, consider the vectors $(3, 2, 0)$ and $(2, -3, 0)$. Their dot product is $(3, 2, 0)\cdot(2, -3, 0) = (3)(2) + (2)(-3) + (0)(0) = 0$. If the angle between the two vectors is less than $90°$, their dot product is a positive number. If the angle is greater than $90°$, the dot product is negative. Thus dot products are helpful for determining whether two vectors are perpendicular, roughly pointing in the same direction, or roughly pointing in opposite directions.
Dot products also depend on the magnitudes of the two vectors: assuming that the dot product is not zero (the case when the vectors are not perpendicular), the larger the magnitude of $\mathbf{A}$ or $\mathbf{B}$ is, the larger the dot product becomes. All of these facts are summarized by the following equation, which relates the angle between any two vectors and their respective magnitudes.
\[ \mathbf{A}\cdot\mathbf{B} = \lvert\mathbf{A}\rvert \lvert\mathbf{B}\rvert \cos(\theta) \]
where $\theta$ is the angle between $\mathbf{A}$ and $\mathbf{B}$. If you are rusty on trigonometry, the $\cos(\theta)$ part is read "cosine of theta." For now, all you need to know is that:
I will explain the cosine and sine trigonometry functions in more detail later.
Another important question we will need to answer about two vectors is, what directions in space are perpendicular to both vectors? This question does not make sense in all cases. If either of the vectors has zero magnitude (i.e., is $(0,0,0)$), there is no meaningful notion of another vector being parallel or perpendicular to it. Also, if the angle between two vectors is $0°$ (they both point in exactly the same direction) or $180°$ (they point in exactly opposite directions, as shown in Figure 4.5), there are an infinite number of directions perpendicular to both.
| |
|
But if both vectors have positive magnitudes and the angle between them is somewhere between $0°$ and $180°$, then there is a unique plane that passes through both vectors. In order for a third vector to point in a direction perpendicular to both $\mathbf{A}$ and $\mathbf{B}$, that vector must be perpendicular to this plane. In fact, there are only two such directions, and they lie on opposite sides of the plane. If the vector $\mathbf{C}$ points in one of these perpendicular directions, then $-\mathbf{C}$ points in the other, as shown in Figure 4.6.
| |
|
Finding a vector like $\mathbf{C}$ would answer our original question, regardless of the magnitude of $\mathbf{C}$: it would point in a direction at right angles to both $\mathbf{A}$ and $\mathbf{B}$.
There is a formula for calculating a perpendicular vector $\mathbf{C}$ from any two vectors $\mathbf{A}$ and $\mathbf{B}$, though it is more complicated than the dot product formula. It is called a cross product, named after the "$\times$" in the conventional math notation "$\mathbf{A}\times\mathbf{B}$". Without derivation in this book, here is the formula for the cross product:
\begin{align*} \mathbf{A}\times\mathbf{B} &= (A_x, A_y, A_z)\times(B_x, B_y, B_z) \\ &= (A_y B_z - A_z B_y, A_z B_x - A_x B_z, A_x B_y - A_y B_x) \end{align*}
If we let $\mathbf{C} = \mathbf{A}\times\mathbf{B}$, then $\mathbf{C}$ points in the direction as shown in Figure 4.6. The cross product taken in the other order, $\mathbf{B}\times\mathbf{A}$, points in the opposite direction, and is in fact equal to $-\mathbf{C}$. To visualize the direction of $\mathbf{C} = \mathbf{A}\times\mathbf{B}$ for any two vectors $\mathbf{A}$ and $\mathbf{B}$, imagine yourself oriented in space such that $\mathbf{A}$ is on your right and $\mathbf{B}$ is on your left. (This might require your body to be sideways or even upside-down, but fortunately this is only in your imagination!) Then $\mathbf{C} = \mathbf{A}\times\mathbf{B}$ will point the same way as the top of your head. Cross products share one trait with dot products: they get "bigger" as the magnitude of $\mathbf{A}$ or $\mathbf{B}$ increases. But a cross product is a vector, not a scalar like the dot product. Another difference is that the dot product of two perpendicular vectors is zero, but the cross product of two perpendicular vectors maximizes the magnitude of their cross product. If both $\lvert\mathbf{A}\rvert > 0$ and $\lvert\mathbf{B}\rvert > 0$, the only way to get a cross product with a zero magnitude is when $\mathbf{A}$ and $\mathbf{B}$ are pointing in exactly the same ($0°$) or exactly opposite ($180°$) directions. The general formula for a cross product's magnitude is
\[ \lvert\mathbf{A}\times\mathbf{B}\rvert = \lvert\mathbf{A}\rvert\lvert\mathbf{B}\rvert \sin(\theta) \]
Compare this to the formula relating the dot product and the included angle $\theta$. Just as $\cos(\theta)$ is zero when $\theta = 90°$, $\sin(\theta)$ is zero when $\theta = 0°$ or $180°$.
If you are new to trigonometry, or you once knew it but have forgotten everything, this section will help. There is a lot to the subject of trigonometry, but I will cover only the essentials you will need for understanding the ray tracing topics covered in this book. Specifically, we will explore the sine and cosine functions and learn a simple way to visualize what they mean.
Let's start with a circle on the $xy$ plane whose radius is 1 unit and centered at the origin $(0, 0)$, as shown in Figure 4.7.
| |
|
If we draw a line at an angle $\theta$ measured counterclockwise from the $+x$ axis and find the point $\mathbf{P}$ where that line crosses the circle, then $\cos(\theta)$ is the point's $x$ coordinate (how far $\mathbf{P}$ is to the right or left of the origin) and $\sin(\theta)$ is the point's $y$ coordinate (how far $\mathbf{P}$ is above/below the origin). If $\mathbf{P} = (P_x, P_y)$, then $P_x = \cos(\theta)$, read "P sub x equals cosine of theta," and $P_y = \sin(\theta)$, read "P sub y equals sine of theta." So if you want to know, for example, when $\cos(\theta)$ is zero, ask yourself what angles $\theta$ could be to make $\mathbf{P}$ neither to the left nor right of the origin. If we are talking about $\theta$ being the angle between two vectors, $\theta$ must be in the range $0° ... 180°$, and therefore for $P_x$ to be zero, $\mathbf{P}$ must be at $(0, +1)$, forcing $\theta$ to be $90°$.