Radio circuits built by Don Cross
Reflex AM receiver – August 2009
I am very pleased to report that I have finally built a radio receiver that is
good enough that I can enjoyably use it!
This receiver is a modification of Charles Wenzel's
Two Transistor Reflex Radio.
Instead of a ferrite AM loopstick antenna, I use a magnetic loop antenna, and I added an
LM386
amplifier stage to drive an 8-ohm speaker. There is a switch to select whether this
amplifier should be used to power the speaker or whether crystal earphone listening is desired.
I use six AA rechargeable NiMH batteries to provide the 8V power supply,
but a 9V alkaline battery or a 6V lantern battery work just fine.
I think even a small solar cell array would suffice to power this thing if you were
camping on a sunny enough day!
 |
|
Prototype receiver on breadboard.
I will soon move all parts currently mounted on the breadboard to a soldered circuit board.
I will also add interface connections with screws on the wood base, so that I can
swap out other receiver modules to the same wooden box.
|
 |
|
Update – 25 August 2009. The finished AM receiver.
The detector and audio amplifier circuitry is now soldered to a permanent circuit board.
I added a handle to make it easy to carry the radio around.
|
 |
|
Close up view of the inside of the finished receiver.
I have the schematics folded up inside a small zipper-style plastic bag, attached to
the inside of the wood frame using Velcro.
The screw connections facilitate removing the circuit board and replacing it
with other experimental designs.
|
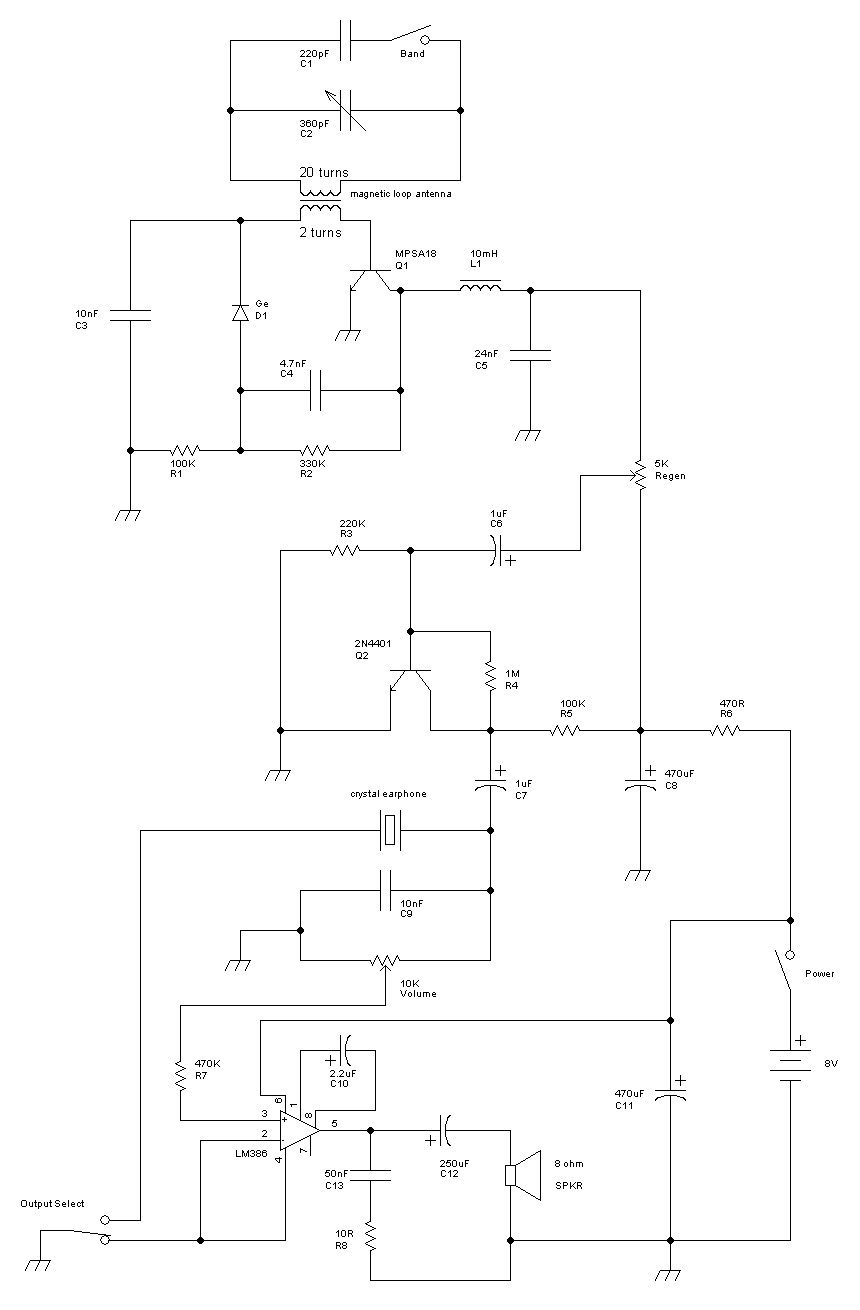
Notes about this circuit
-
The magnetic loop antenna is depicted as a transformer.
It is actually a pair of hand-wound rectangular loops of enameled magnet wire,
about 5.5 inches by 4.5 inches.
If I build another one of these receivers, I will wrap maybe 16 or 18 turns instead of 20
on the tuner side to bring down the inductance so that I can tune higher on the AM band.
-
The antenna is highly directional. You have to rotate the radio to aim it at the
desired radio station. More specifically, for strongest reception of a
nearby station (i.e. not receiving by skywave propagation)
the radio station must lie in the plane of the loop, and that plane must
be at right angles to the ground. (Apparently the magnetic component
is polarized horizontally.) If you rotate the radio 180° around
a vertical axis, its reception of a given station will be the same.
This directionality can be used to advantage. Where I live there are
two radio stations close together in frequency: 1030kHz and 1060kHz.
However, it is fortunate for me that they are about 60 degrees apart
in terms of compass direction from my house.
Selectivity of this receiver is pretty good, and with proper aiming I can
almost completely block out one of the two stations and focus on the other.
I even put felt feet on the bottom of the chassis (the kind used on chair legs to prevent
scuffing the floor), so that I can easily spin the radio around without scratching
the table it is on!
UPDATE (27 August 2009): Try out my
online Azimuth/Distance calculator page
to determine the exact compass direction and distance of a radio station!
Use Google Maps or Google Earth to find
your exact latitude and longitude. Use this as "Point A" in the calculator.
Use the
FCC online AM radio station database
to find the coordinates of the transmitter. Use this as "Point B".
The calculated azimuth tells you how many degrees clockwise from North the station is
from your location.
-
The Band switch selects whether you are tuning the lower or higher end of the AM broadcast band.
When the 220pF capacitor C1 is connected in parallel with the tuning capacitor, the tuner can
reach down to well below 540kHz. With C1 disconnected, the tuner can reach as high as 1100 kHz.
Where I live there aren't any stations I care about above this frequency, but in the future
the aforementioned decrease in the number of turns in the magnetic loop antenna should
better fit the AM band.
-
The Output Select switch (see lower left in schematic) toggles between driving the
high-impedance crystal earphone or the 8-ohm speaker via the LM386 amplifier.
In earphone mode, the receiver draws a miserly 1.5mA of battery current; that could
make your battery last for hundreds of hours! (At least, I think so. I am still
in the process of testing practical battery life with my NiMH rechargeable batteries.)
In speaker mode, the current consumption is more like 8mA to 15mA, depending on the
volume setting.
-
When the Output Select is set for earphone mode, the Volume knob has no effect.
Use the Regen to get the best volume you can without distortion.
You won't get head-banging rock concert volume, but you will be able to hear talk
radio quite clearly.
-
In speaker mode, you need to adjust both the Regen and Volume knobs to get proper balance
between volume and distortion.
-
If the 470K resistor R7 is replaced with a wire, you get problems with oscillations
(so-called "motor-boating"). Looking at the
LM386 data sheet,
I see that there is a 50K resistance between
the amplifier's positive and negative inputs. Apparently R7 limits the audio-frequency
current flowing through C7 enough to stabilize the circuit.
When I started this project, I had a wire instead of R7 and I was trying to figure out
how to fix the oscillation problem. I disconnected the wire and noticed that if I touched
one of my fingers to the wiper pin of the Volume potentiometer, and another finger to
pin 3 of the LM386, the radio suddenly started working! I played around with various
resistors in the range 100K to 1M and settled on 470K as a good value.
If you build this receiver, try various values; another might work better for you.
-
The potentiometer I use for the Volume knob has a built-in SPDT switch.
I use this as my power switch: when Volume is turned all the way down, it clicks off.
-
My design is a lot bulkier than is really needed, but I did this on purpose
to make future experimentation easier. I want a lot of room for my large hands to
move around! I want to be able to re-use the chassis, antenna, and controls for
other experimental circuits, so I'm designing it to allow the receiver circuit
board to be swapped out with other designs.
-
The LM386 data sheet gives an example value of 10µF for the capacitor I call C10
in the schematic. I started out with this value, but I found the audio to sound
"muddy" when the volume knob was turned up too high. In fact, there was
a tendency to oscillate past a certain point.
After experimenting, I settled on 2.2µF as a better fit.
It reduces bass while leaving midrange and treble strong, and allows better fidelity
sound at higher volume settings. I tried as low as 0.2µF, but at that point
the sound was too tinny and wasn't capable of the volume level I wanted.
Experimental determination of inductance L and parasitic capacitance Cx
Tonight (28 August 2009) I had fun with an experiment to figure out the inductance
of the tuning coil (the 20 turns of magnet wire), along with its so-called "parasitic" capacitance.
I tuned the receiver to 6 different radio stations.
For each radio station, I turned the receiver off, disconnected one of the tuning capacitor wires,
and measured the tuning capacitor with my capacitance meter.
Now in each case, I know both the frequency of the radio station f
and the tuning capacitance Ct.
If you look at the schematic above, you will note that the 220pF capacitor labeled C1 (which I will call Cf here)
can be included or excluded from the tuning circuit, using the "band" switch.
I was able to tune two of the radio stations (WDBO and WORL)
with either band switch setting, because they broadcast on frequencies included in the overlap of both bands.
I recorded the band switch setting in all measurements. Overall, I took a total of 8 measurements of
the 6 stations, with WDBO and WORL having 2 measurements each (one for each band switch position).
My goal was to solve for two unknowns: inductance L and parasitic capacitance Cx.
The total capacitance of the tank circuit is
C = Ct + BCf + Cx
where B indicates the state of the band switch:
when that switch is closed, the capacitor Cf is included and B=1.
When the switch is open, Cf is excluded and B=0.
The relationship between frequency, total capacitance, and inductance is
LC = 1012 / (2πf)2
The factor of 1012 is needed to correct for the fact that f is expressed in kHz
and LC is expressed in pF*μH. If "pure" units of Hz, F, and H were used,
this numerator would simply be 1. The squared reciprocal of kHz makes the answer
106 times bigger than it would have been with Hz, because now we are dividing
by a number that is a million times smaller (a thousand squared).
By definition, there are 1012 pF in one farad, and
106 μH in one henry. Putting all of this together, we get a correction factor of
10(12 + 6 − 6) = 1012.
I made a spreadsheet that used this formula to calculate the value of LC for each station frequency f,
recorded the tuning capacitor Ct measurements, and had a box where I could
modify my guess for the value of Cx.
When I divide the calculated value of the product LC by the total capacitance
C, I get a theoretical value for the inductance L.
By trial and error, I settled on an optimal value for Cx = 38.5pF,
and modified the nominal value of Cf to be 223pF to make all the L values
as close together as possible.
Here is table that shows what my spreadsheet looks like:
| station |
f [kHz] |
LC [pF*μH] |
Ct [pF] |
B |
C [pF] |
L [μH] |
| WFLF |
540 |
86867 |
218 |
1 |
479.5 |
181.16 |
| WDBO |
580 |
75298 |
155 |
1 |
416.5 |
180.79 |
| WDBO |
580 |
75298 |
378 |
0 |
416.5 |
180.79 |
| WORL |
660 |
58150 |
65 |
1 |
326.5 |
178.10 |
| WORL |
660 |
58150 |
288 |
0 |
326.5 |
178.10 |
| WYGM |
740 |
46257 |
221 |
0 |
259.5 |
178.25 |
| WONQ |
1030 |
23876 |
91 |
0 |
129.5 |
184.37 |
| WSDO |
1400 |
12924 |
33 |
0 |
71.5 |
180.75 |
Based on these data, I have the following estimates:
L = (180.2 ± 4.6) μH
Cx ≈ 38.5 pF
I used two standard deviations around the mean value for the uncertainty of L.
(Update: 9 September 2009) I realized I should go back and measure the
resistance of the magnetic loop antenna. It turns out to be 3.0 Ω.
This kind of analysis should help me design better hand-wound magnetic loop antennas in the future.
Ideally, I may be able to design a tuner that doesn't need a band switch to cover the entire AM band.
Another possibility is that I may be able to design a tuner that uses a variable inductor instead
of a variable capacitor to tune to various stations.
In general, it will be interesting to compare experimentally determined coil behavior with
the values I get from the various formulas for estimating inductance based on coil geometry.
Links




