[back to Cosine Kitty's math page]
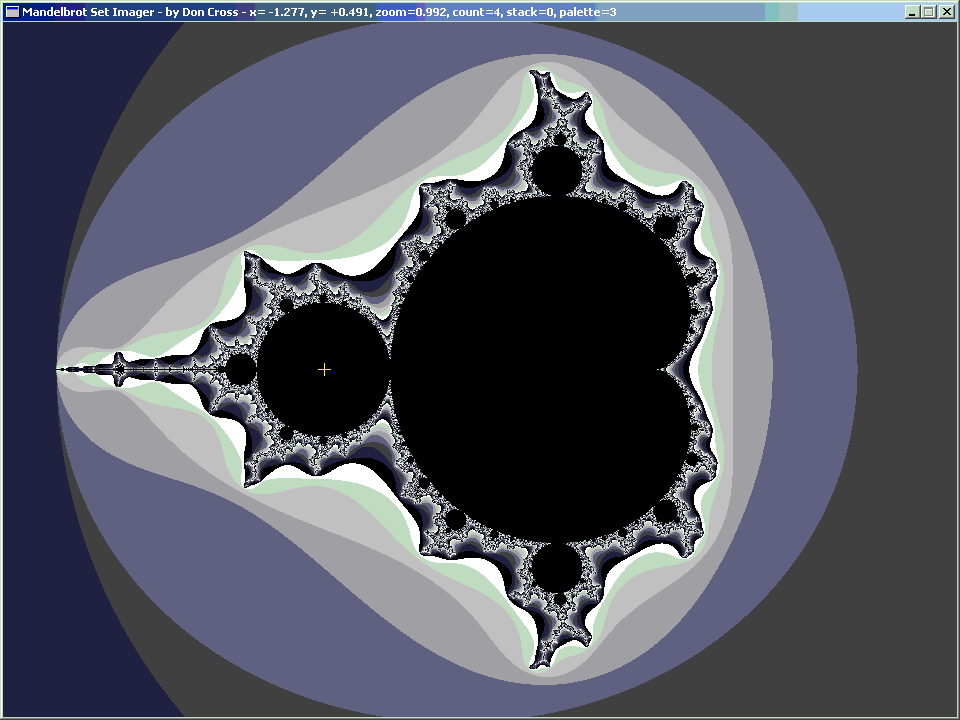
I made an interesting discovery today (29 January 2005). I realized that it is possible to look at the Mandelbrot Set in a different way. Usually it is graphed by iterating the formula
and coloring each complex-valued pixel c based on how long it takes to escape a circle of radius 2. The resulting image looks like this:

| z[0] = 0 |
| z[1] = z[0]2 + c = 02 + (−1) = −1 |
| z[2] = z[1]2 + c = (−1)2 + (−1) = 0 |
| z[3] = z[2]2 + c = 02 + (−1) = −1 |
| z[4] = z[3]2 + c = (−1)2 + (−1) = 0 |
| ... |
My own home-brew Mandelbrot Set imager now allows me to type in an arbitrary algebraic expression f(z) in terms of the complex variable z, and generates a fractal based on iterating Newton's Method to find a solution for f(z)=0.
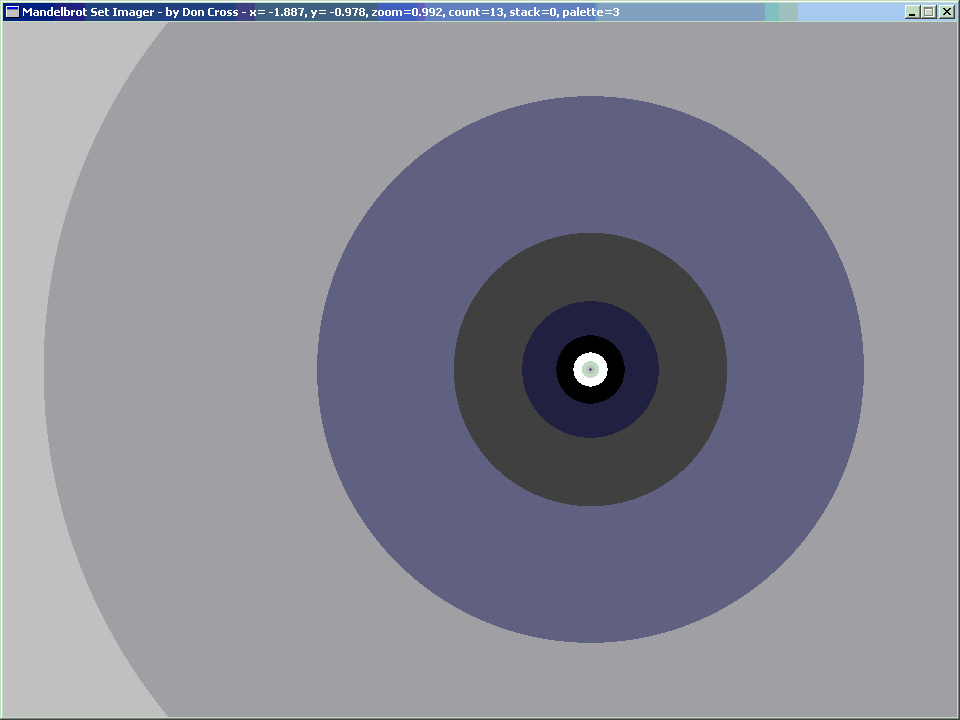
It occurred to me that it would be interesting to graph solutions for various orbital periods in the Mandelbrot formula. For example, if I wanted to find places where the Mandelbrot formula repeated every iteration (i.e. orbital period = 1), I would solve for z2 + z = z, or z2 = 0. Of course, this is a trivial case, since it is obvious that the only solution is z=0.
As one might expect, a trivial formula yields a trivial image, in this case not even a fractal... just a set of concentric circles:
 | ||||
|
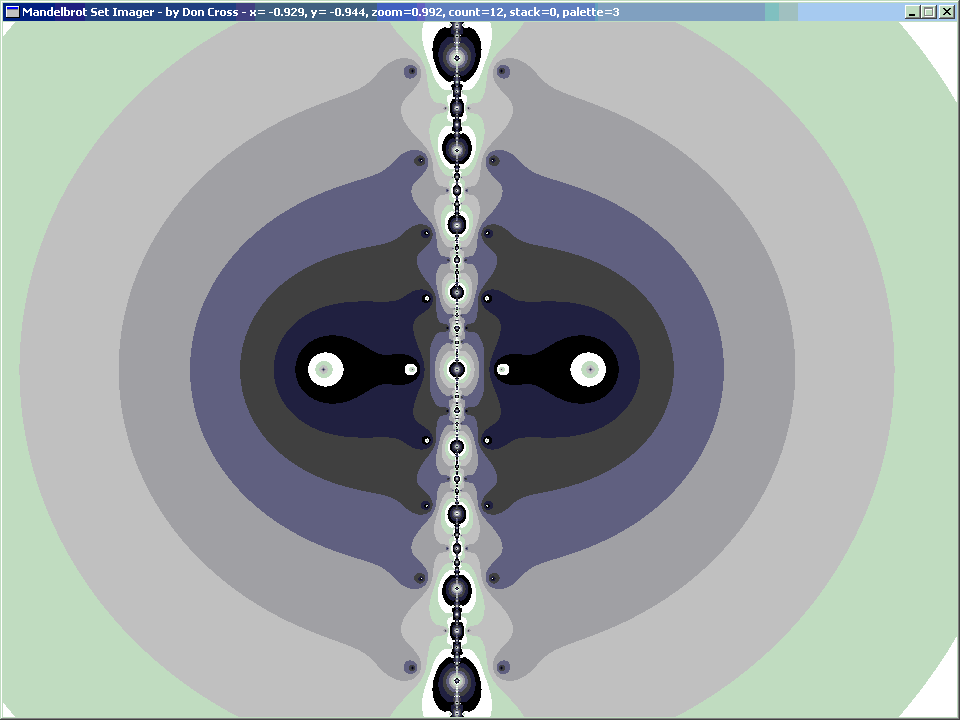
For the orbital period of 2, we get our first non-trivial image. This time it is a fractal. The solutions are z = +1 and z = −1, which show up as the larger horizontal eyes. This is interesting, but there is no resemblance of the Mandelbrot Set (yet).
 | ||||||
|
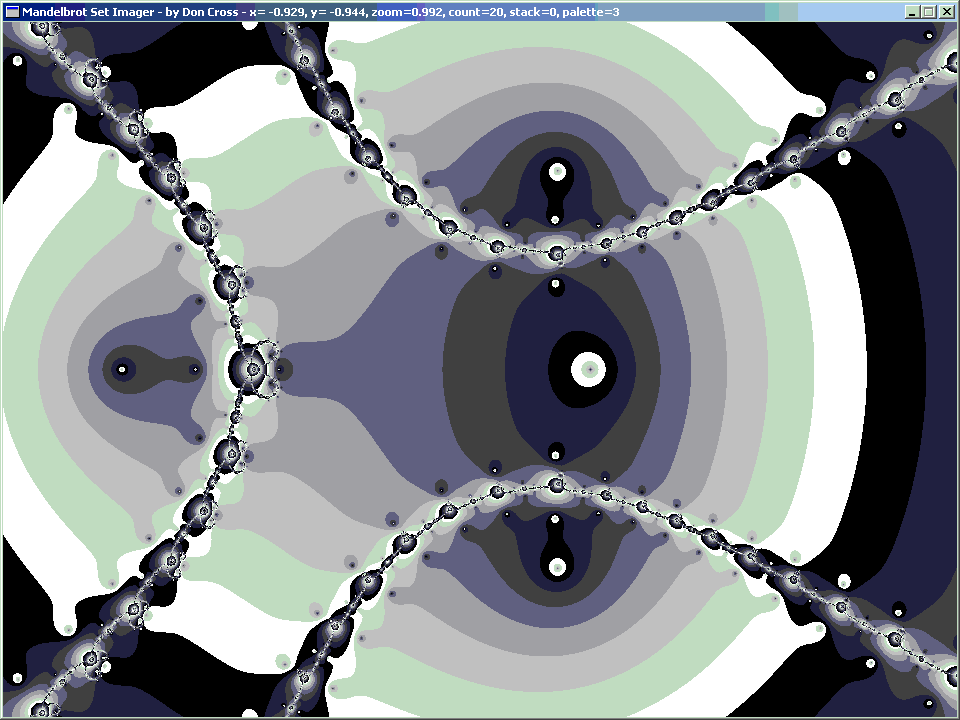
Now at orbital period 3, something interesting happens: we are starting to see a definite pear shape.
Also, because of the Fundamental Theorem of Algebra, there are 2p−1 complex solutions, where p is the orbital period, because each higher orbital period corresponds with a polynomial based on squaring the previous period's polynomial. The reason it is 2p−1 and not 2p is because when the orbital period is 1, there is only 1 solution, and 1 = 20.
 | ||||||||
|
 | ||||||||||||||
|
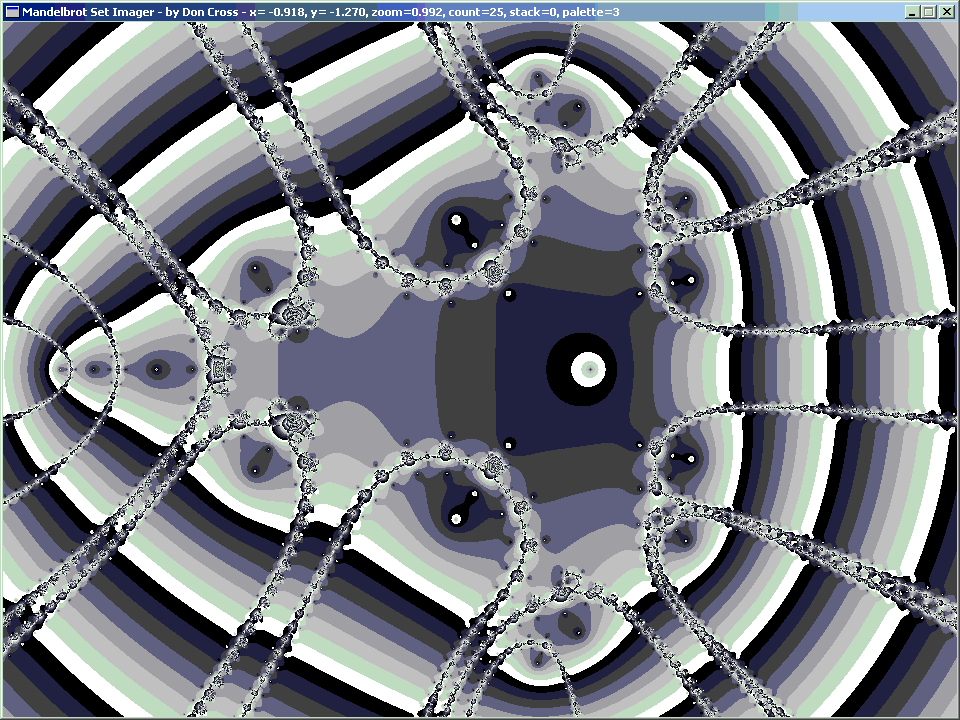 | ||||||||||||||||||||||
|
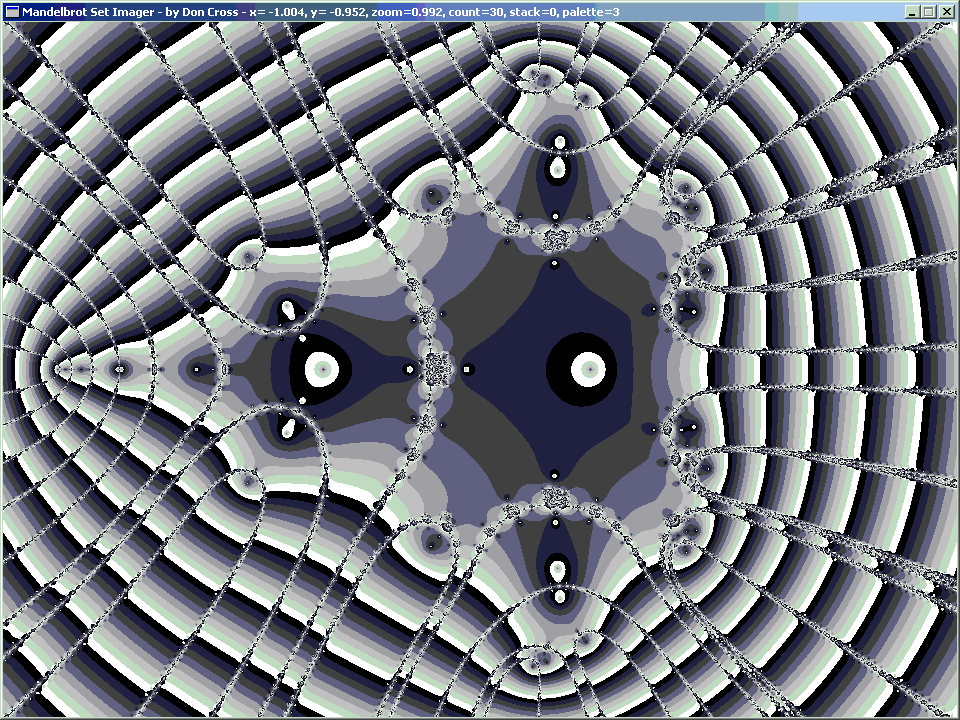 | ||||||||||||||||||||||||||||||||||||||||||
|
 |
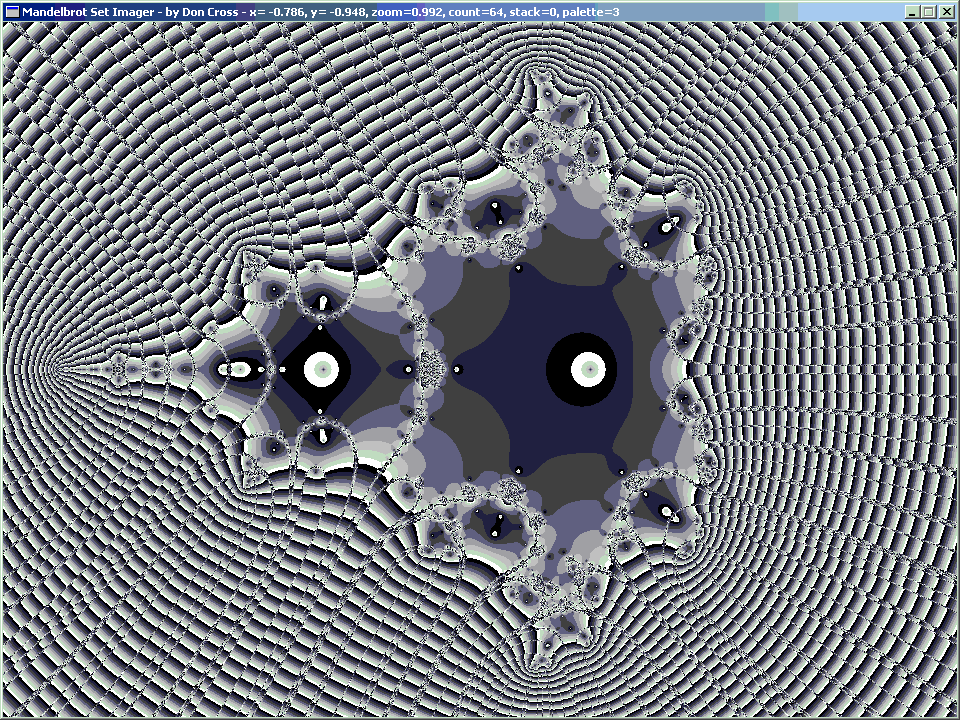 |